Kiam temas priantenoj, la demando, kiu plej zorgigas homojn, estas "Kiel efektive atingiĝas radiado?" Kiel la elektromagneta kampo generita de la signalfonto disvastiĝas tra la transmisilinio kaj ene de la anteno, kaj fine "disiĝas" de la anteno por formi ondon en libera spaco.
1. Unuopa drata radiado
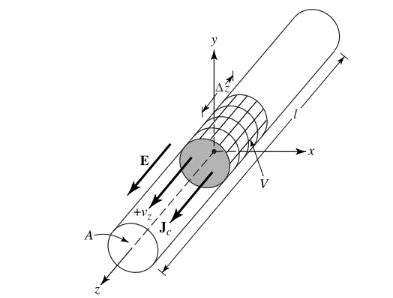
Ni supozu, ke la ŝarga denseco, esprimita kiel qv (Kulombo/m³), estas unuforme distribuita en cirkla drato kun transversa areo de a kaj volumeno de V, kiel montrite en Figuro 1.
Figuro 1
La tuta ŝargo Q en volumeno V moviĝas en la direkto z kun uniforma rapido Vz (m/s). Oni povas pruvi, ke la kurentdenseco Jz sur la transversa sekco de la drato estas:
Jz = qv vz (1)
Se la drato estas farita el ideala konduktilo, la kurentdenseco Js sur la dratsurfaco estas:
Js = qs vz (2)
Kie qs estas la surfaca ŝarga denseco. Se la drato estas tre maldika (ideale, la radiuso estas 0), la kurento en la drato povas esti esprimita kiel:
Iz = ql vz (3)
Kie ql (kulombo/metro) estas la ŝargo por unuo de longo.
Ni ĉefe okupiĝas pri maldikaj dratoj, kaj la konkludoj validas por la supre menciitaj tri kazoj. Se la kurento varias laŭ tempo, la derivaĵo de formulo (3) rilate al tempo estas jena:
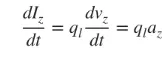
(4)
az estas la akcelo de ŝargo. Se la longo de la drato estas l, (4) povas esti skribita jene:
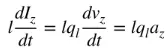
(5)
Ekvacio (5) estas la baza rilato inter kurento kaj ŝargo, kaj ankaŭ la baza rilato de elektromagneta radiado. Simple dirite, por produkti radiadon, devas esti tempo-varia kurento aŭ akcelo (aŭ malakcelo) de ŝargo. Ni kutime mencias kurenton en tempo-harmoniaj aplikoj, kaj ŝargo plej ofte estas menciita en pasemaj aplikoj. Por produkti ŝargan akcelon (aŭ malakcelon), la drato devas esti fleksita, faldita kaj malkontinua. Kiam la ŝargo oscilas en tempo-harmonia moviĝo, ĝi ankaŭ produktos periodan ŝargan akcelon (aŭ malakcelon) aŭ tempo-varian kurenton. Tial:
1) Se la ŝargo ne moviĝas, ne estos kurento nek radiado.
2) Se la ŝargo moviĝas kun konstanta rapido:
a. Se la drato estas rekta kaj senfina laŭ longo, ne estas radiado.
b. Se la drato estas fleksita, faldita, aŭ malkontinua, kiel montrite en Figuro 2, ekzistas radiado.
3) Se la ŝargo oscilas laŭlonge de la tempo, la ŝargo radiiĝos eĉ se la drato estas rekta.
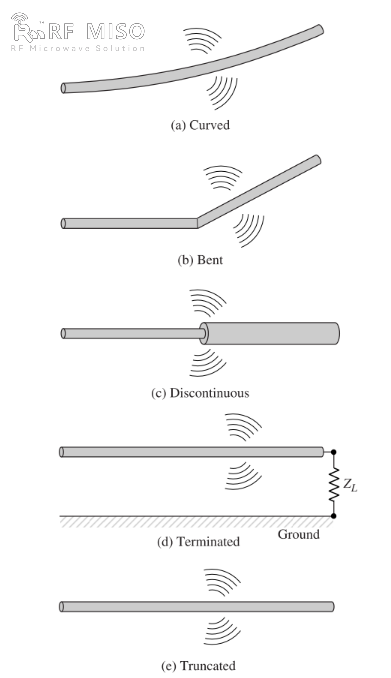
Figuro 2
Kvalitan komprenon pri la radiada mekanismo oni povas akiri per rigardo al pulsa fonto konektita al malferma drato, kiu povas esti terkonektita tra ŝarĝo ĉe ĝia malferma fino, kiel montrite en Figuro 2(d). Kiam la drato estas komence energiigita, la ŝargoj (liberaj elektronoj) en la drato estas ekmovataj de la elektraj kampolinioj generitaj de la fonto. Ĉar la ŝargoj estas akcelitaj ĉe la fonta fino de la drato kaj malakcelitaj (negativa akcelo relative al la originala movo) kiam reflektitaj ĉe ĝia fino, radiada kampo estas generita ĉe ĝiaj finoj kaj laŭlonge de la resto de la drato. La akcelo de la ŝargoj estas plenumata per ekstera fonto de forto, kiu ekigas la ŝargojn kaj produktas la asociitan radiadan kampon. La malakcelo de la ŝargoj ĉe la finoj de la drato estas plenumata per internaj fortoj asociitaj kun la induktita kampo, kiu estas kaŭzita de la amasiĝo de koncentritaj ŝargoj ĉe la finoj de la drato. La internaj fortoj akiras energion de la amasiĝo de ŝargo dum ĝia rapido malpliiĝas al nulo ĉe la finoj de la drato. Tial, la akcelo de la ŝargoj pro la ekscito de la elektra kampo kaj la malakcelo de la ŝargoj pro la malkontinueco aŭ glata kurbo de la drata impedanco estas la mekanismoj por la generado de elektromagneta radiado. Kvankam kaj kurentdenseco (Jc) kaj ŝargdenseco (qv) estas fontaj termoj en la ekvacioj de Maxwell, ŝargo estas konsiderata pli fundamenta kvanto, precipe por pasemaj kampoj. Kvankam ĉi tiu klarigo de radiado estas ĉefe uzata por pasemaj statoj, ĝi ankaŭ povas esti uzata por klarigi konstantan radiadon.
Rekomendi plurajn bonegajnantenaj produktojfabrikita deRFMISO:
2. Du-drata radiado
Konekti tensiofonton al du-konduktila transmisilinio konektita al anteno, kiel montrite en Figuro 3(a). Apliki tension al la du-drata linio generas elektran kampon inter la konduktiloj. La elektraj kampolinioj agas sur la liberajn elektronojn (facile apartigeblajn de atomoj) konektitajn al ĉiu konduktilo kaj devigas ilin moviĝi. La movado de ŝargoj generas kurenton, kiu siavice generas magnetan kampon.
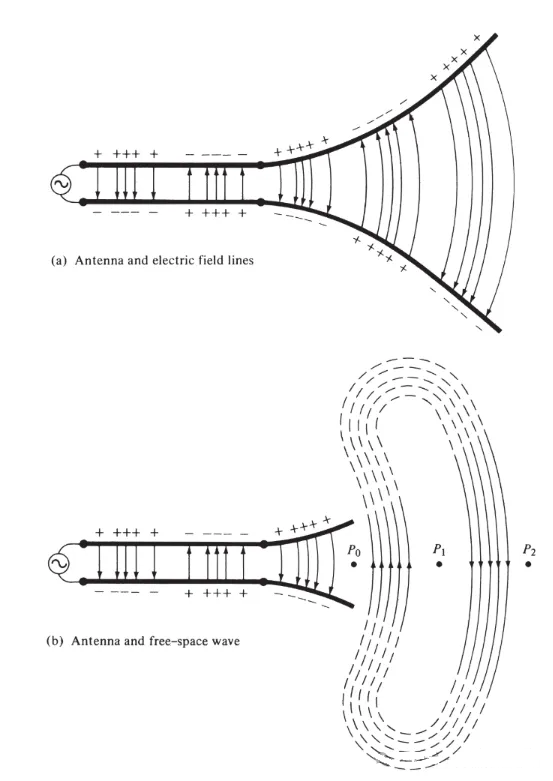
Figuro 3
Ni akceptis, ke elektraj kampolinioj komenciĝas per pozitivaj ŝargoj kaj finiĝas per negativaj ŝargoj. Kompreneble, ili ankaŭ povas komenciĝi per pozitivaj ŝargoj kaj finiĝi ĉe infinito; aŭ komenciĝi ĉe infinito kaj finiĝi per negativaj ŝargoj; aŭ formi fermitajn buklojn, kiuj nek komenciĝas nek finiĝas per iuj ŝargoj. Magnetaj kampolinioj ĉiam formas fermitajn buklojn ĉirkaŭ kurent-portantaj konduktiloj, ĉar ne ekzistas magnetaj ŝargoj en fiziko. En iuj matematikaj formuloj, ekvivalentaj magnetaj ŝargoj kaj magnetaj kurentoj estas enkondukitaj por montri la duecon inter solvoj implikantaj potencon kaj magnetajn fontojn.
La elektraj kampolinioj desegnitaj inter du konduktiloj helpas montri la distribuon de ŝargo. Se ni supozas, ke la tensiofonto estas sinusoida, ni atendas, ke la elektra kampo inter la konduktiloj ankaŭ estu sinusoida kun periodo egala al tiu de la fonto. La relativa grando de la elektra kampa intenseco estas reprezentita per la denseco de la elektraj kampolinioj, kaj la sagoj indikas la relativan direkton (pozitivan aŭ negativan). La generado de tempo-variaj elektraj kaj magnetaj kampoj inter la konduktiloj formas elektromagnetan ondon, kiu disvastiĝas laŭ la transmisilinio, kiel montrite en Figuro 3(a). La elektromagneta ondo eniras la antenon kun la ŝargo kaj la koresponda kurento. Se ni forigas parton de la antenstrukturo, kiel montrite en Figuro 3(b), liberspaca ondo povas esti formita per "konektado" de la malfermaj finoj de la elektraj kampolinioj (montritaj per la punktitaj linioj). La liberspaca ondo ankaŭ estas perioda, sed la konstanta-faza punkto P0 moviĝas eksteren je la lumrapideco kaj vojaĝas distancon de λ/2 (al P1) en duona tempoperiodo. Proksime al la anteno, la konstanta-faza punkto P0 moviĝas pli rapide ol la lumrapideco kaj alproksimiĝas al la lumrapideco ĉe punktoj malproksimaj de la anteno. Figuro 4 montras la liberspacan elektran kampodistribuon de la λ∕⁶ anteno ĉe t = 0, t/8, t/4, kaj 3T/8.
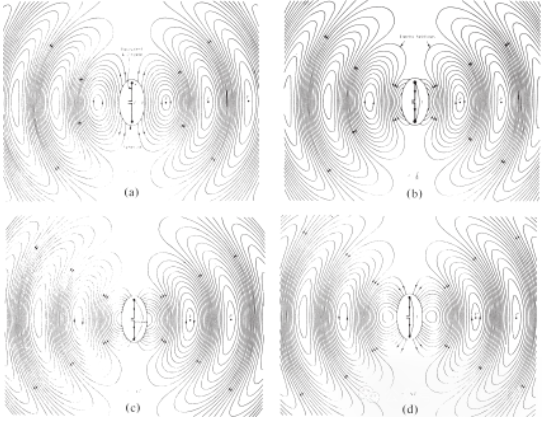
Figuro 4 Distribuo de la elektra kampo en libera spaco de la λ∕2 anteno ĉe t = 0, t/8, t/4 kaj 3T/8
Oni ne scias kiel la gviditaj ondoj estas apartigitaj de la anteno kaj fine formitaj por disvastiĝi en libera spaco. Ni povas kompari gviditajn kaj liberspacajn ondojn kun akvondoj, kiujn povas kaŭzi ŝtono faligita en trankvilan akvejon aŭ alimaniere. Post kiam la perturbo en la akvo komenciĝas, akvondoj estas generitaj kaj komencas disvastiĝi eksteren. Eĉ se la perturbo ĉesas, la ondoj ne ĉesas sed daŭre disvastiĝas antaŭen. Se la perturbo daŭras, novaj ondoj konstante generiĝas, kaj la disvastiĝo de ĉi tiuj ondoj postrestas kompare kun la aliaj ondoj.
La samo validas por elektromagnetaj ondoj generitaj de elektraj perturboj. Se la komenca elektra perturbo de la fonto estas mallongdaŭra, la generitaj elektromagnetaj ondoj disvastiĝas ene de la transmisilinio, poste eniras la antenon, kaj fine radias kiel liberaj ondoj, eĉ se la ekscito jam ne ĉeestas (same kiel la akvondoj kaj la perturbo, kiun ili kreis). Se la elektra perturbo estas kontinua, la elektromagnetaj ondoj ekzistas kontinue kaj sekvas ilin proksime dum disvastiĝo, kiel montrite en la bikonusa anteno montrita en Figuro 5. Kiam elektromagnetaj ondoj estas ene de transmisilinioj kaj antenoj, ilia ekzisto rilatas al la ekzisto de elektra ŝargo ene de la konduktilo. Tamen, kiam la ondoj estas radiataj, ili formas fermitan buklon kaj ne estas ŝargo por subteni ilian ekziston. Ĉi tio kondukas nin al la konkludo, ke:
Ekscito de la kampo postulas akcelon kaj malakcelon de la ŝargo, sed bontenado de la kampo ne postulas akcelon kaj malakcelon de la ŝargo.
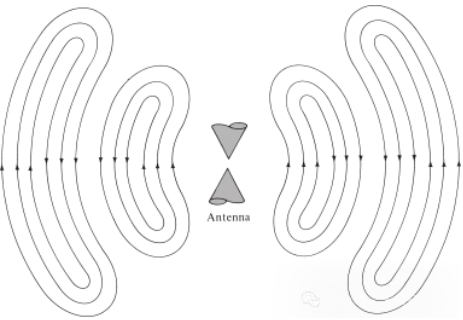
Figuro 5
3. Dipola Radiado
Ni provas klarigi la mekanismon per kiu la elektraj kampolinioj liberiĝas de la anteno kaj formas liberspacajn ondojn, kaj prenu la dipolan antenon kiel ekzemplon. Kvankam ĝi estas simpligita klarigo, ĝi ankaŭ ebligas al homoj intuicie vidi la generadon de liberspacaj ondoj. Figuro 6(a) montras la elektrajn kampoliniojn generitajn inter la du brakoj de la dipolo kiam la elektraj kampolinioj moviĝas eksteren je λ∕4 en la unua kvarono de la ciklo. Por ĉi tiu ekzemplo, ni supozu, ke la nombro de formitaj elektraj kampolinioj estas 3. En la sekva kvarono de la ciklo, la originalaj tri elektraj kampolinioj moviĝas pliajn λ∕4 (entute λ∕2 de la komenca punkto), kaj la ŝarga denseco sur la konduktilo komencas malpliiĝi. Oni povas konsideri, ke ĝi estas formita per la enkonduko de kontraŭaj ŝargoj, kiuj nuligas la ŝargojn sur la konduktilo ĉe la fino de la unua duono de la ciklo. La elektraj kampolinioj generitaj de la kontraŭaj ŝargoj estas 3 kaj moviĝas distancon de λ∕4, kio estas reprezentita per la punktitaj linioj en Figuro 6(b).
La fina rezulto estas, ke estas tri malsupreniraj elektraj kampolinioj en la unua λ∕4 distanco kaj la sama nombro da supreniraj elektraj kampolinioj en la dua λ∕4 distanco. Ĉar ne estas neta ŝargo sur la anteno, la elektraj kampolinioj devas esti devigitaj disiĝi de la konduktilo kaj kombiniĝi por formi fermitan buklon. Ĉi tio estas montrita en Figuro 6(c). En la dua duono, la sama fizika procezo estas sekvata, sed notu, ke la direkto estas kontraŭa. Post tio, la procezo estas ripetata kaj daŭras senfine, formante elektran kampodistribuon similan al Figuro 4.
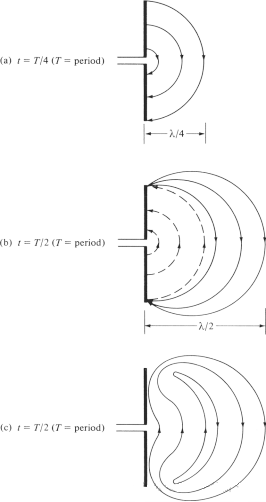
Figuro 6
Por lerni pli pri antenoj, bonvolu viziti:
Afiŝtempo: 20-a de junio 2024










